Líneas (rectas)

Ejercicio

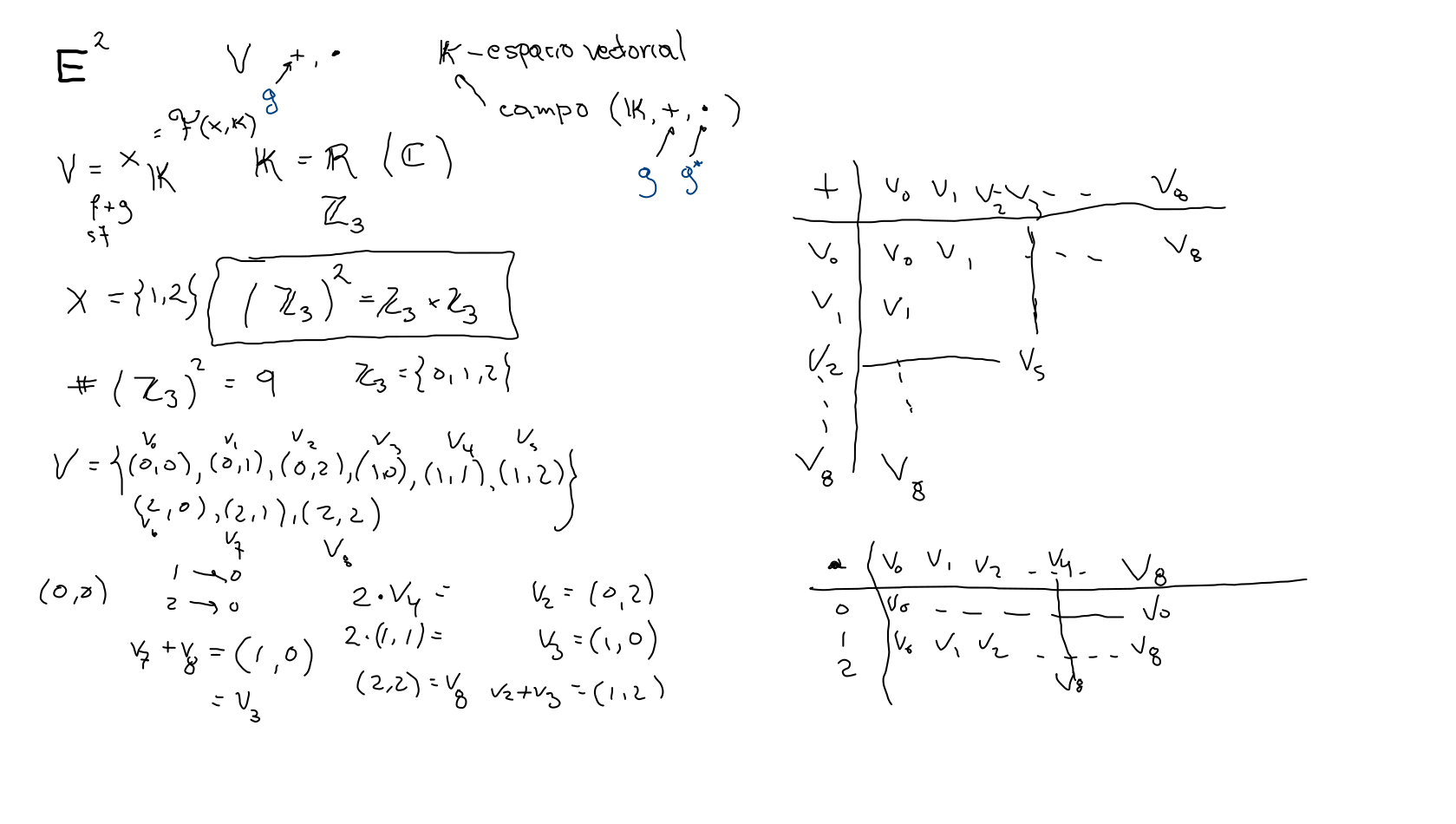
$\R^n$ modelo

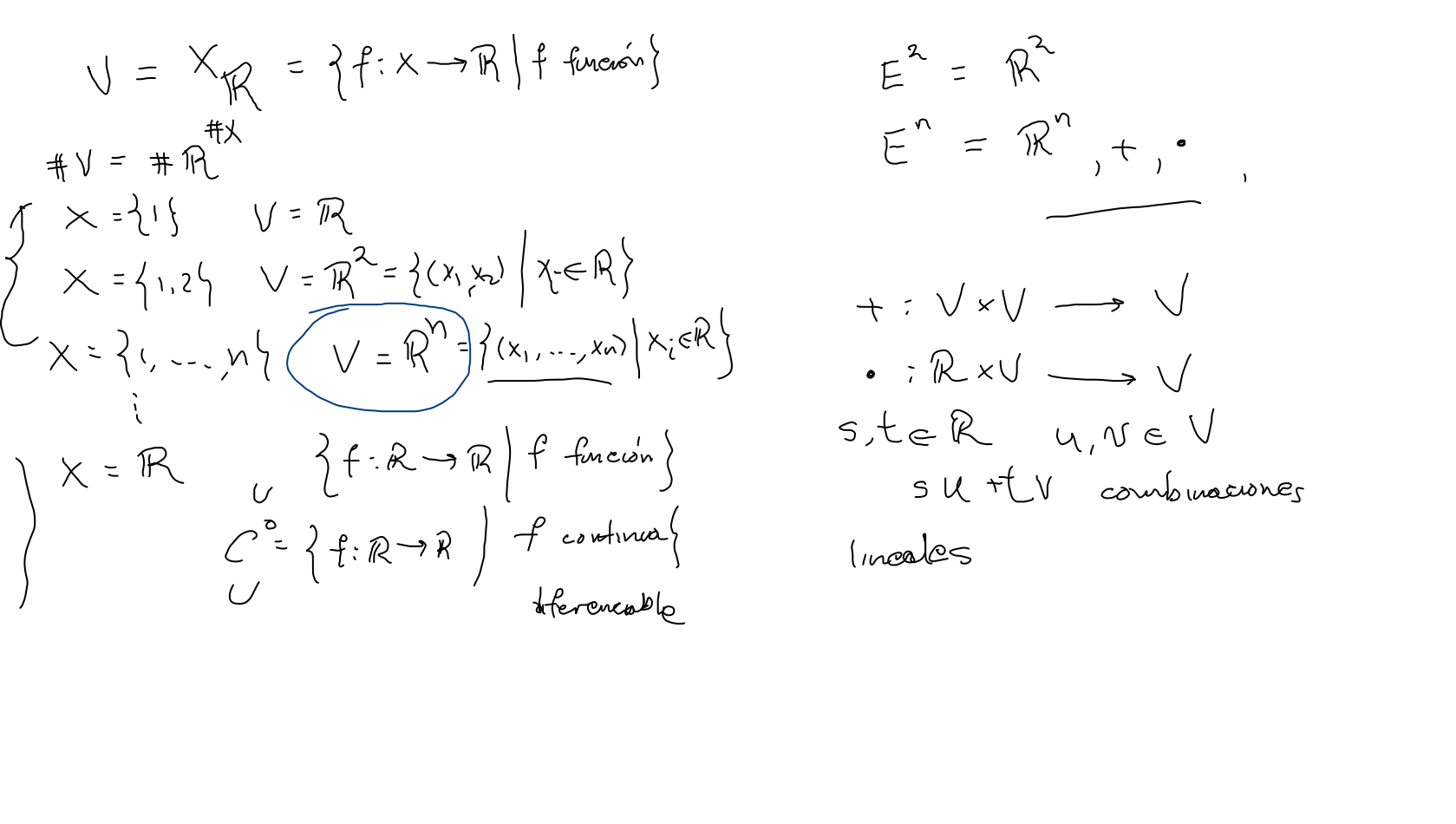
Líneas

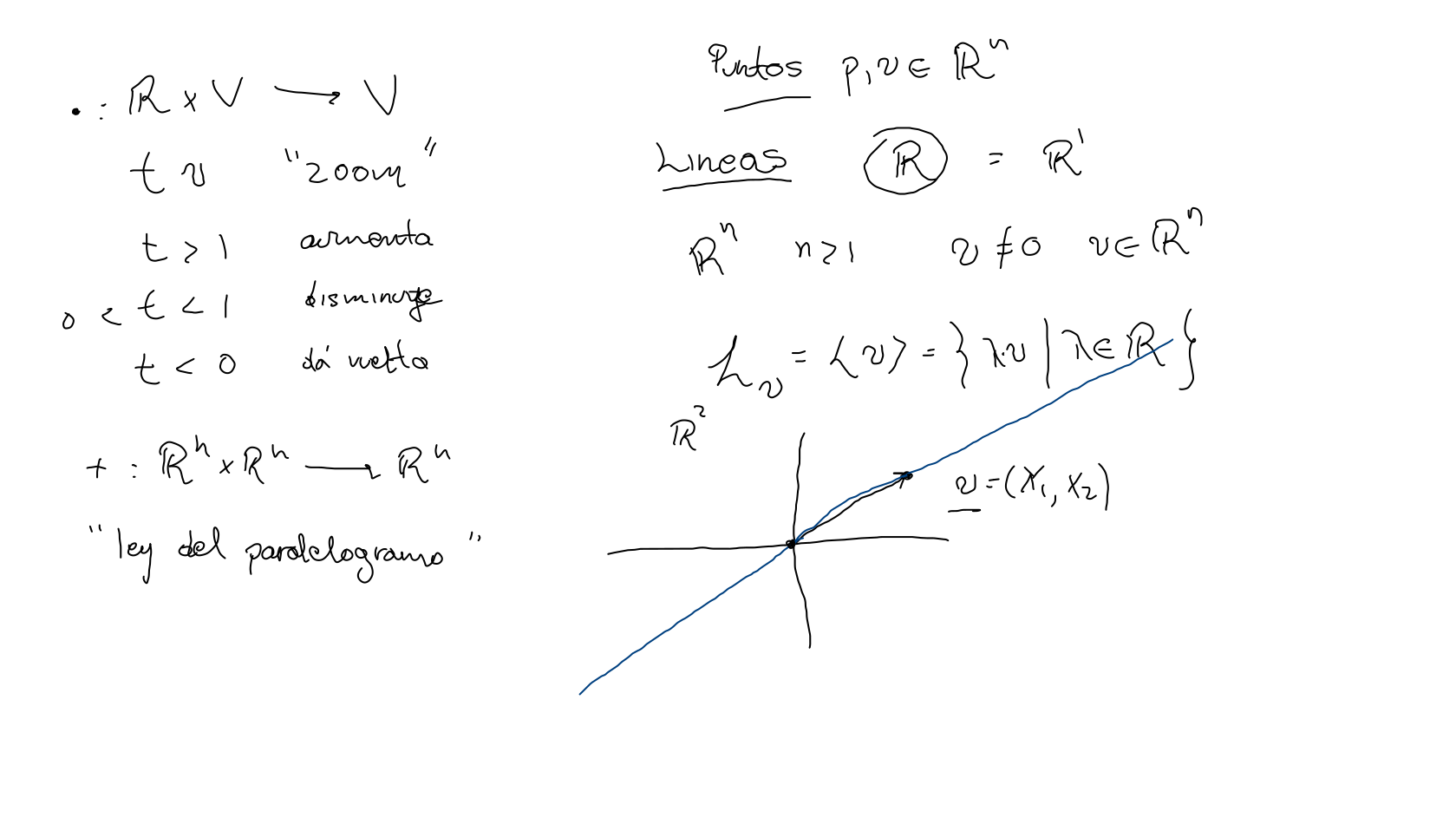
Elemento básico $\mathbb{R}=\mathbb{R}^1$, la recta real.

Dado un vector $\mathbf u$ (velocidad), podemos considerar la línea recta o movimiento rectilíneo uniforme de una partícula en origen $\mathbf O$ con velocidad $\mathbf u$ (distinta de cero).

Este conjunto de puntos se obtiene al escalar el vector $\mathbf u$ con todas las escalas posibles, denotamos:

$$\mathcal{L}_\mathbf{u}=\langle\mathbf{u}\rangle=\{t\mathbf{u}\vert t\in\mathbb{R}\}$$

Representación paramétrica

Si la partícula que describe la línea recta no está situada en el orígen sino en el punto $P$, empujamos la línea simplemente sumando $P$.

Tenemos así para $\mathbf u, P\in\mathbb R^n (\mathbb R^2)$

Definición La línea recta $\mathcal L$ en dirección del vector $\mathbf u$ que pasa por el punto $P$ está dada por

$$\mathcal L=\{P+t\mathbf u\vert t\in\mathbb R\}\subset\mathbb R^n$$